Constructivist Learning Design

What is the Constructivist Learning Design?

According to Schroeder and Lester (1989), there are three approaches to mathematical problem solving: (1) Teaching for Problem Solving, (2) Teaching about Problem Solving, and (3) Teaching through Problem Solving. The Constructivist Learning Design (CLD) is one interpretation of how teaching through problem solving can be enacted in Singapore mathematics classrooms.

 

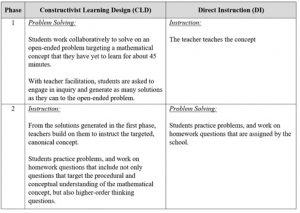
The CLD draws upon three effective learning designs which were already tested in Asian classrooms: Productive Failure (Kapur, 2008), the Open-Ended Approach (Becker & Shimada, 1997), and the Post-Tea House Teaching Approach (Tan, 2013). Unlike direct instruction (DI), whereby students were first taught a new concept and its related procedures before solving problems related to the concept, the CLD reverses the sequence and proposes a framework which outlines two essential and sequential phases – Problem Solving phase and Instruction phase – in structuring consecutive lessons. The Table below describes the two instructional phases in CLD and contrasts them with DI.

 

 

What does the Constructivist Learning Design seek to accomplish?

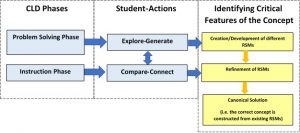
The Problem Solving phase in CLD allows for activation of prior knowledge and experiences as students engage in carefully designed problems, tasks, or activities aimed at eliciting a diversity of knowledge structures. The student-generated solutions, known as Representations and Solution Methods (RSMs; Kapur & Bielaczyc, 2012), mark students’ preliminary constructions and understanding of the targeted concept. RSMs can be intuitive constructions at first. More sophisticated, formal mathematical RSMs can be developed as students move from individual attempts to co-constructions during group discussions facilitated by the teacher. The Instruction phase serves as a purposeful platform for focused discussions where students are encouraged to analyse and compare the variety of solution pathways or RSMs created earlier, often with teacher facilitation.

 

During the two phases of CLD, students engage in four main actions: explore-generate, compare-connect (see Figure below; Ng et al., 2020). Explore-generate are actions students undertake when they experiment with scenarios, cases, and examples of events presented in the problem. A range of mathematical arguments, computations, and representations are thus generated or constructed as RSMs. Compare-connect are actions which take place naturally during discussions because selected RSMs are compared and analysed for their affordances and constraints in encompassing the critical features of the concept. Students may draw connections between cases and across sets of prior knowledge as they look for similarities and differences amongst the RSMs. The double arrow between explore-generate and compare-connect signals the likely cyclical nature of these processes in each phase as part of development and refinement of RSMs.